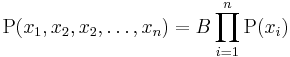Product form solution
In probability theory, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product form solution has algebraic form
where B is some constant. Solutions of this form are of interest as they are computationally inexpensive to evaluate for large values of n. Such solutions in queueing networks are important for finding performance metrics in models of multiprogrammed and time-shared computer systems.
Equilibrium distributions
The first product form solutions were found for equilibrium distributions of Markov processes. Trivially, models composed of two or more independent sub-components exhibit a product form solution by the definition of independence. Initially the term was used in queueing networks where the sub-components would be individual queues. For example, Jackson's theorem gives the joint equilibrium distribution of an open queueing network as the product of the equilibrium distributions of the individual queues.[1] After numerous extensions, chiefly the BCMP network it was thought local balance was a requirement for a product form solution.[2][3] Gelenbe's G-network model showed this to not be the case.[4] Product form solutions are sometimes described as "stations are independent in equilibrium".[5]
The search for processes with product form solutions continues as an active research area in queueing theory and other Markovian settings such as Markov process algebras (e.g. PEPA[6][7]) and stochastic timed petri nets. J.M. Harrison and R.J. Williams note that "virtually all of the models that have been successfully analyzed in classical queueing network theory are models having a so-called product form stationary distribution"[5]
Sojourn time distributions
The term product form has also been used to refer to the sojourn time distribution in a cyclic queueing system, where the time spent by jobs at M nodes is given as the product of time spent at each node.[8] In 1957 Reich showed the result for two M/M/1 queues in tandem,[9] later extending this to n M/M/1 queues in tandem[10] and to overtake–free paths in Jackson networks.[11] Walrand and Varaiya suggest that non-overtaking (where customers cannot overtake other customers by taking a different route through the network) may be a necessary condition for the result to hold.[11] Mitrani offers exact solutions to some simple networks with overtaking, showing that none of these exhibit product form sojourn time distributions.[12]
For closed networks, Chow showed a result to hold for two service nodes[13], which was later generalised to a cycle of queues[14] and to overtake–free paths in Gordon–Newell networks.[15][16]
References
- ^ Jackson, James R. (1963). "Jobshop-like queueing systems". Management Science 10 (1): 131–142. doi:10.1287/mnsc.10.1.131.
- ^ Boucherie, Richard J.; van Dijk, N. M. (1994). "Local balance in queueing networks with positive and negative customers". Annals of Operations Research 48: 463–492. doi:10.1007/BF02033315.
- ^ Chandy, K. Mani; Howard, J. H., Jr; Towsley, D. F. (1977). "Product form and local balance in queueing networks". Journal of the ACM 24: 250–263. doi:10.1145/322003.322009.
- ^ Gelenbe, Erol (1993). "G-Networks with triggered customer movement". Journal of Applied Probability 30 (3): 742–748. doi:10.2307/3214781.
- ^ a b Harrison, J. M.; Williams, R. J. (1992). "Brownian models of feedforward queueing networks: quasireversibility and product form solutions". Annals of Applied Probability 2 (2): 263–293. doi:10.1214/aoap/1177005704.
- ^ Hillston, Jane (1999). "Product form solution for a class of PEPA models". Performance Evaluation 35 (3–4): 171–192. doi:10.1016/S0166-5316(99)00005-X.
- ^ Harrison, P. G. (2003). "Turning back time in Markovian process algebra". Theoretical Computer Science 290: 1947–1986. doi:10.1016/S0304-3975(02)00375-4.
- ^ Boxma, O. J.; Kelly, F. P.; Konheim, A. G. (January 1984). "The Product Form for Sojourn Time Distributions in Cyclic Exponential Queues". Journal of the ACM 31 (1). doi:10.1145/2422.322419.
- ^ Reich, E. (1957). "Waiting Times when Queues are in Tandem". The Annals of Mathematical Statistics 28 (3): 768–773. doi:10.1214/aoms/1177706889.
- ^ Reich, E. (1963). "Note on Queues in Tandem". The Annals of Mathematical Statistics 34: 338. doi:10.1214/aoms/1177704275.
- ^ a b Walrand, J.; Varaiya, P. (1980). "Sojourn Times and the Overtaking Condition in Jacksonian Networks". Advances in Applied Probability 12 (4): 1000–1018. doi:10.2307/1426753.
- ^ Mitrani, I. (1985). "Response Time Problems in Communication Networks". Journal of the Royal Statistical Society. Series B (Methodological) 47 (3): 396–406. JSTOR 2345774.
- ^ Chow, We-Min (April 1980). "The Cycle Time Distribution of Exponential Cyclic Queues". Journal of the ACM 27 (2). doi:10.1145/322186.322193.
- ^ Schassberger, R.; Daduna, H. (1983). "The Time for a Round Trip in a Cycle of Exponential Queues". Journal of the ACM 30: 146. doi:10.1145/322358.322369.
- ^ Daduna, H. (1982). "Passage Times for Overtake-Free Paths in Gordon-Newell Networks". Advances in Applied Probability 14 (3): 672–686. doi:10.2307/1426680.
- ^ Kelly, F. P.; Pollett, P. K. (1983). "Sojourn Times in Closed Queueing Networks". Advances in Applied Probability 15 (3): 638–656. doi:10.2307/1426623.